大数据 | 大数据基础--算法之亚线性时间算法：计算图的平均度算法一

亲爱的读者朋友大家晚上好，前几篇文章我们介绍了点集合的直径和连通分量的数量等几个问题，这次我们来分析图的平均度的计算，这个问题的定义非常简单。

定义

已知：\(G=(V,E)\)

求：平均度\(\bar{d} = \frac{\sum_{u\in V}d(u)}{n}\)

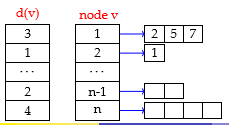
假设：\(G\)是简单图，没有平行边和自环；\(G\)由邻接链表和存储度数的数组表示，如图中的\(d(v),node(v)\)所示。

1601198667811

分析

对于一些特殊的图，如\(n-cycle\ graph\)，就是说这个图就是一个长度为\(n\)的环，这样的图的平均度就是2。对于\(clique\ graph\)，也就是图中的一个局部完全子图，比如说\((n-c\sqrt{n})-cycle + c\sqrt{n}-clique\ graph\)，它的平度\(\bar{d} \approx 2 + c^2\)，这个计算非常简单，请自行进行推导。

但是对于一个通常的图就需要一个通用的方法，最简单的可以用随机采样的方法，也就是在图中随机选择\(s\)个点，求这些点的度的平均值，就是最后的估计值。当然了方法很简单，但是算出的结果也很粗糙。

下面我们来看一个看起来比较正常的算法，算法的idea是这样的：将具有相似或者相同度数的节点分组，然后估算每个分组的平均度数。

首先我们来将所有的点进行分桶，分成\(t\)个桶，第\(i\)个桶里的点集合为\(B_i=\{v|(1+\beta)^{(i-1)} < d(v) < (1+\beta)^{i}\},0<i\leq t-1\)，其中\(\beta\)是超参数。

于是\(B_i\)中的点的总度数有上下界如公式所示：\((1+\beta)^{(i-1)}|B_i| < d(B_i) < (1+\beta)^{i}|B_i|\)。

进一步地\(G\)的总度数可以表示为：\(\sum_{i=0}^{t-1}(1+\beta)^{(i-1)}|B_i| < \sum_{u\in V}d(u) < \sum_{i=0}^{t-1}(1+\beta)^{i}|B_i|\)。

于是我们可以得到：\(\frac{\sum_{i=0}^{t-1}(1+\beta)^{(i-1)}|B_i|}{n} < \bar{d} < \frac{\sum_{i=0}^{t-1}(1+\beta)^{i}|B_i|}{n}\)。

经过这样的转化，我们就将问题转化成了对\(\frac{B_i}{n}\)的估计，计算的算法如下。

算法

1. 从\(V\)取出样本集合\(S\)
2. \(S_i \gets S \cap B_i\)
3. \(\rho_i \gets \frac{S_i}{S}\)
4. 返回\(\hat{\bar{d} } = \sum_{i=0}^{t-1}\rho_i(1+\beta)^{i}\)

算法的思想其实很简单，将\(\frac{B_i}{n}\)理解为一种概率，就是随机选一个点，这个点属于\(B_i\)的概率，这样理解算法就很简单了。

评价

算法的思想和计算都很简单，只是进行了一个非常巧妙的转化，但是这个算法仍然是有问题的，这将会在下周一的文章中指出并提出新的算法来解决问题，敬请期待。